梦幻西游玩家用所学知识解析梦幻 网友建议直接充钱

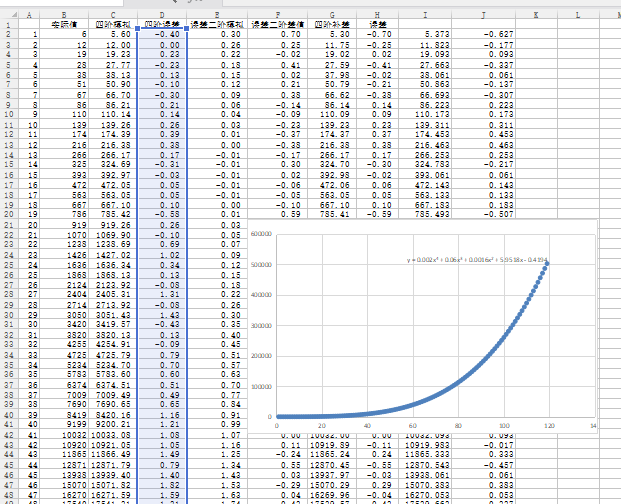
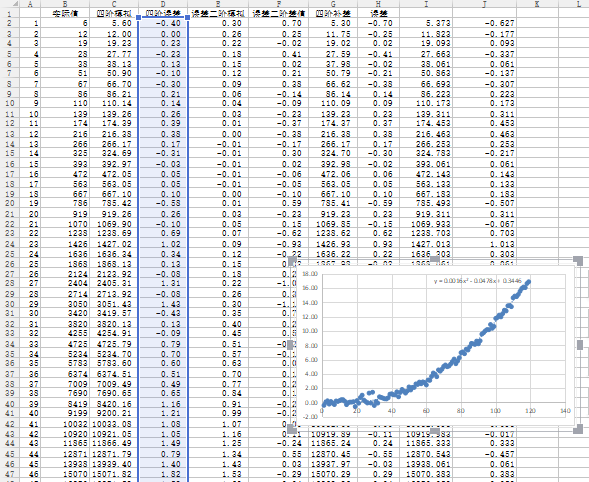
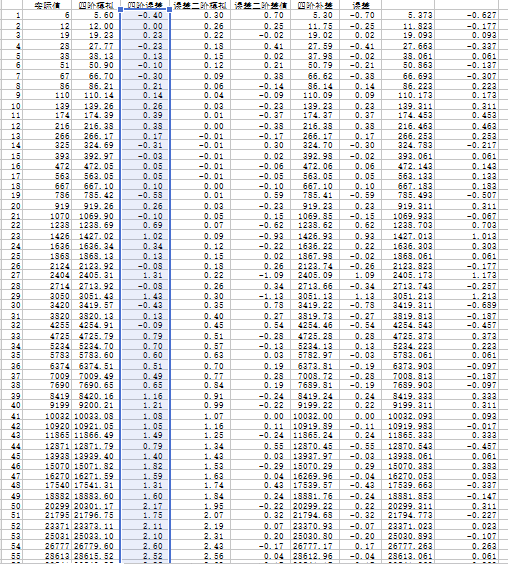
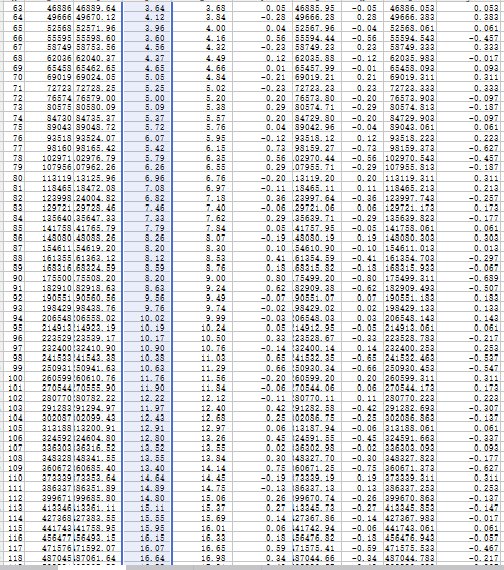
　　可以在趋势线里选择“多项式”，并填写项数，一步到位。

　　当然并不是一步到位，我详细写一下这一种方法：

　　第一步：列表，插入散点图，增加趋势线，得到的是y1= 0.002x4 + 0.06x3 + 0.0016x2 + 5.9518x - 0.4194。

　　这已经模拟的很好了，其实够用了，结束。

　　第二步：如果我们追求更精确，那么我们将新的四阶函数输入到新的一栏，得到理论值，用原始数据和四阶理论值求差，得到误差，当s较小的时候，误差也很小，如图所示，但你们看不到的部分，到100左右时，误差达到了16点(误差16其实已经很小了，要知道建邺捡一次钱都有100)。

　　第三步：误差列插入散点图(如图所示)。

　　第四步：这样得到了误差的函数图像，显然这是一个二次函数，我们用二次多项式去模拟，得到其趋势线为：y2 = 0.0016x2 - 0.0478x + 0.3446。

　　第五步：用刚刚得到的y1减去这里的误差y2，得到新的补差函数，其函数为y3= 0.002x4 + 0.06x3 + 5.9996x - 0.764。

　　第六步：我们将y3= 0.002x4 + 0.06x3 + 5.9996x - 0.764稍微调整，把一次项系数变成整数6，带入求值列表，并求误差。

　　第七步：将误差求平均值，用y3减去这个值，得到真正的y=0.002x^4+0.06x^3+6x-0.689。

　　带入求值，得到最终的理论值，然后求误差，发现误差都在1以下，都是零点几的误差，如图所示：

　　第二列为原始数据，倒数第二列为最终函数的理论值，最后一栏为最后的误差，都不足1。

　　由此，我们得到了g-s函数关系式!g=0.002s^4+0.06s^3+6s-0.689。

　　【技术第二章：求解思路】

　　先剧透一下，我最终会用c++写一段代码，思路是这样的：

　　比如女儿村，他的输出Dpr(damage per round)受很多因素影响，就目前我知道的，有：目标个数N(number of attack)、门派技能S1(master skill)、暗器技能S2(skill of hidden weapon)、武器伤害(包括伤害符合太阳石)W(weapon damage)、敏捷属性A(agility)、灵饰固伤O(ornament)、阵法加成F(formation)、法术修炼Pm(practice of magic)、法抗修炼Pr(practice of resistance)、符石R(rune)、固伤符F(Fu Wen of Shenmulin)、暗器命中H(hidden weapon)。

　　我们得到的函数是一个Dpr关于N、S1、S2、W、A、O、F、Pm、Pr、R、F、H的12元函数。

　　而每一个参数，都和金钱g有关，我们可以模拟出每一个参数和在这一项上花的金钱gi的函数关系：

　　g1=g1(S1)(师门技能上消耗的金钱和技能等级的关系，第一章我们给出了)，g2=g2(S2)，g3=g3(W)，……

　　然后我们对所有的gi进行求和，g=g1+g2+g3+...+g12。

　　那么我们给定一个g值，必然有一个最大的Dpr，每一个g及其对应的最大的Dpr，构成一个函数，这是我们需要的。

　　这个函数的意思是：如果我投入一个确定的资金，我能达到的最大的每回合伤害之间的函数关系。

　　其实这是一个非线性规划的题目，g=g1+g2+……+g12为约束方程，Dpr=f(gi)为规划方程。

　　那么我们如何处理这个非线性规划呢?

　　我的方法是这样的：

　　第一步：初始化，取函数Dpr=f(gi)，约束方程g=sum(gi)，其中g=gi=0，Dpr=D。

　　第二步：用Dpr=f(gi)对每一个参数gi求偏导，得到12个方程d1=d1(g1)，d2=d2(g2)，...di=di(gi)。

　　第三步：令g=g+1。(自变量取下一个。)

　　第四步：将gi带入每一个di中，求各自的偏导值di1。(算在当前情况下每一个项目所能增加的伤害值。)

　　第四步：比较每一个di1，取最大值，假设当i=k时求得最大值dk1。(这里的意思是把钱花到第k的项目上，提高的伤害最大。)

　　第五步：令gk=gk+1。(把钱分配到gk上去。)

　　第六步：将新的gk带入到原函数里求新的Dpr。

　　第七步：输出所有数据。

　　第八步：重复第三步到第七步。

　　由此，最终我们可以求解出最佳的充值路径。

　　而且可以得到当我们充值金额为某一个确定值时，所能取得的最大伤害量，并得到其对应的在每一个项目上分配的金额和提升的水平。

　　搞定!

　　思路就是这样，接下来的几天我会详细描述每一个环节，并最终用Microsoft visual c++写出代码，然后用计算机算出我的最佳路径。

　　那么在本思路中，有很多难题，我们已经在第一章里示范了S1与g1的关系，同样的，S2和g2之间的关系也可以求。

　　但是还有很多函数关系我们并没有得到，比如武器伤害W和g3之间的关系，这显然是非线性的，而且不好估测。我会以我们区的物价为基准，且以109级为标准，列一个W和g3的关系，就是说109级的装备伤害与价格之间的关系，例如W=10，10点伤害就是0级武器，那么对应的g3=500。当然低级武器可以以NPC价格为参考，而高级一点的，或者超过国标部分的伤害，可能就会是一个非常不精确的平均估值，例如109所带的初伤为600的武器的价格，就是500伤最便宜的无级别的价格。最终这个W值是有上限的，而g没有上限，所以当g3趋于无穷大的时候，W趋于某个确定的值，即150WJB满伤627(不考虑专用)。

　　如果我们连个非线性非多项式的函数关系就找到了，整个课题就简单得多了。