梦幻西游玩家用所学知识解析梦幻 网友建议直接充钱
|
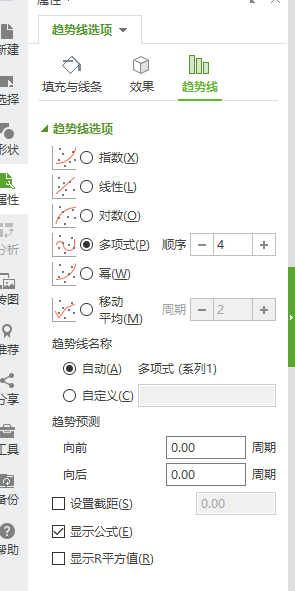
我们知道,任何一款游戏,都少不了数值策划,那数值策划的世界里满满的都是数据么?今天有玩家就想挑战一下,直接用自己四年所学知识展开分析,看看策划在游戏中是如何决策的,分析的内容包含函数构造、多元函数偏微分与非线性规划,大部分玩家看完后都直呼你告诉我们该充多少钱吧!大家说说,这玩家毕业后具备去网易上班的潜质么? 故事回到一周前的一个夜晚,我和女友正在肝饥荒,这已经是我们第n次重新开档,异地恋除了肝游戏,还能gan点啥?奈何主机不给力,网络上行速度又跟不上,自建服务器卡成狗,我又不忍心让她卡,只能让她当主机,卡得我要哭了,她又只会捡东西,我又卡,根本混不过冬天... 于是我就跟她说:要不然我们玩梦幻吧! 回想起初中时代的梦幻时光,那是我最美好的回忆之一,那时候玩过飞燕女(女儿村),还玩过舞天姬(龙宫),玩109舞天姬还和初中最好的哥♂们结婚三年,那是一段令(bu)人(kan)怀(hui)念(shou)的时光。 (此处省略一万字) 所以我就胡汉三又回来了!! 情怀党当然是选择自己练,目前在世界之窗,女友单开,我四开。 刚进入游戏,我就懵逼了——这个游戏是怎么玩的? 于是我打算用本科四年所学的知识,去解读这个游戏,顺便分享给可爱的猪友。 但是我转念一想,均满修满技能150WJB17段,根本不需要什么分析,只需要加大充值力度,决策什么的,好像没啥用。就当萌新自嗨吧。 进入正题!我主要是介绍一些常用的数据分析和处理的方法,当然我自己也会慢慢地更新一些实际处理的结论。 队伍图镇!(手机上就这一张图,以后都不会伤害大家的眼睛了) 【技术第一章:如何利用数据模拟多项式函数】 先放结论:技能消耗金钱值g(gold)与技能等级s(skill)之间的关系式为:g=0.002s^4+0.06s^3+6s-0.689。 游戏是以数据为基础的,在代码封闭的情况下,如何利用输出数据,模拟程序内部的函数关系,是游戏数据分析的重要课题,下面介绍一种方法: 我们分析梦幻里每一级师门技能s和对应需要消耗的金钱数g的关系。 首先我们需要拿到输出数据列表,网上有的,官网上也查得到。 我们将之输出到Excel里,如图所示: 这样我们得到了原始数据,虽然实际上这是一个数列Gn,我们也可以近似看作一个可微函数g=f(s)。 但如何得到f(x)的具体表达式呢? 这里有一个针对多项式的专门的方法: 第一步:将原始数据逐项相减,G(s)-G(s-1),得到新的数列。易证:新数列的主项和原函数的导数的主项相同。这样我们得到的数列所对应的新函数g2=f2(s)是原函数g=f(s)的导数,多项式求导次数会降低一次。 第二步:重复第一步的内容,将新函数逐项相减,得到g3、g4、g5...。 第三步:由于原函数g=f(s)是多项式,经过有限次的降次,将得到一次函数y=kx+b,直观上可以通过作图看出数据已经均匀分布在直线上或两侧附近。 第四步:用Excel画出上述一次函数的趋势线,假设我们得到g4为一次函数,其斜率为k=0.048,主项为0.048s。 第五步:积分得到g3,我们知道g4是g3的导数,那么对g3积分,就是g4,这里我们只积主项,因为数列求差和函数求导的主项是一样的,但低阶项会产生误差,显然g3的主项是0.024s^2。 第六步:重复以上步骤,积分得到g的主项,高中知识就告诉我们结果是0.002s^4。这样我们就得到了第一主项。 第七步:列出第一主项的值,用原始数据减第一主项得到误差。 第八步:显然误差是三次的,设误差为p1,我们用p1的各项逐渐相减,用刚刚处理原数列的方法处理p1数列,最终求出p1的主项为0.06s^3,这就是原函数的第二项。 第九步:重复第七步和第八步,求出原函数的所有项。 第十步:将所求所有项相加,得到原函数为:g=0.002s^4+0.06s^3+6s-0.689。 太复杂看不懂?微软知道你可能不会,除此之外,我们还有一个方法: |
本文仅代表发表厂商及作者观点,不代表叶子猪本身观点!



 ID:youximhxy
ID:youximhxy

 群号:1045753197
群号:1045753197